Absolútne čierne teleso (dokonale čierne teleso, čierne teleso), žiarenie (vyžarovanie) čierneho telesa :)

Vytvorené: 08. 03. 2020 Tlačiť

Hypotetické teleso, ktoré pohltí všetko naň dopadajúce elektromagnetické žiarenie. Keďže žiadne žiarenie neodráža ani neprepúšťa, pri bežných teplotách okolia sa javí ako čierne.

Podľa Kirchhoffovho zákona tepelného žiarenia je takéto teleso aj ideálnym žiaričom. Absolútne čierne teleso vyžaruje elektromagnetické žiarenie všetkých frekvencií. Frekvenčné rozdelenie energie vyžiarenej z jeho povrchu závisí len od jeho absolútnej teploty a predstavuje univerzálnu funkciu, ktorá charakterizuje tepelné žiarenie všetkých zohriatych telies.

Energia, ktorú vyžarujú reálne fyzikálne telesá, sa od energie čierneho telesa líši len (frekvenčne závislým) násobným koeficientom (emisivitou ɛ). Pre každé reálne teleso platí ɛ ˂ 1, čo znamená, že pri danej teplote vyžaruje menej energie ako absolútne čierne teleso.

Pojem absolútne čierneho telesa zaviedol okolo 1860 Gustav Robert Kirchhoff (1824-1887), jeho praktickú realizáciu navrhol 1890 Wilhelm Wien (1864-1928). Podľa jeho návrhu možno absolútne čierne teleso dostatočne dobre realizovať ako malý otvor na dutine, ktorá je celá v tepelnej rovnováhe so svojimi stenami. Žiarenie vstupujúce otvorom sa v dutine celé pohltí, keďže fakticky nemá možnosť vrátiť sa otvorom späť.

Absolútne čierne teleso ako abstraktný pojem teoretickej fyziky zohralo dôležitú úlohu vo vývoji fyziky a pri formulovaní základných predstáv rozvíjajúcej sa kvantovej mechaniky.

Žiarenie čierneho telesa

Každé teleso s teplotou vyššou ako je absolútna nula vyžaruje do okolitého priestoru elektromagnetické žiarenie.

Absolútna nula je teplota 0 K, alebo -273,15 °C. Je to teplota, pri ktorej úplne ustáva pohyb častíc látky[1].

Vlnová dĺžka, na ktorej toto teleso najviac vyžaruje, závisí od jeho teploty. Čím väčšia je teplota telesa, tým kratšiu vlnovú dĺžku má žiarenie, ktoré vysiela do priestoru.

Táto vlnová dĺžka sa dá jednoducho vypočítať podľa vzťahu λ_max=b/T, kde b je konštanta b=2,898.10^-3 m . K, a kde T je teplota povrchu telesa v Kelvinoch.

Železný kutáč v tme pri izbovej teplote okolo 20 °C (273 K) neuvidíme. Do okolia vyžaruje elektromagnetické žiarenie s vlnovou dĺžkou s neviditeľného infračerveného žiarenia. Keď ho však začneme zahrievať, začne sa jeho teplota zvyšovať a s ňou sa bude skracovať vlnová dĺžka žiarenia, ktorá pri určitej teplote začne patriť do viditeľnej časti spektra, na ktorú sú citlivé naše oči. Rozžeravený kutáč začne byť vidno, nadobudne červenú farbu. Keby sme ho boli schopní zohriať na stále vyššie teploty[2], sledovali by sme, ako sa jeho farba mení od červenej cez oranžovú a žltú a postupne by nadobudol modravú farbu. Pri ďalšom zohrievaní by bol už tak horúci, že vlnová dĺžka, na ktorej vyžaruje, by bola za viditeľným úsekom spektra a kutáč by vysielal neviditeľné ultrafialové žiarenie a opäť by ho prestalo byť vidno[3].

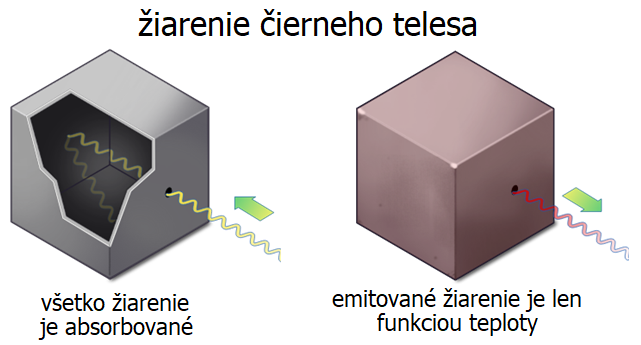
Aby bolo možné jednoducho pracovať so žiarením telies, bol zavedený fyzikálny model: absolútne čierne teleso. Je to idealizované teleso, ktoré dokonale pohltí všetku energiu svetla, ktoré naň dopadá a tú vyšle v podobe tepelného žiarenia. V praxi sa ako čierne teleso správa napríklad dutina so začiernenými vnútornými stenami a malým otvorom, z ktorého žiarenie vystupuje.

Rozloženie žiarenia čierneho telesa na jednotlivých vlnových dĺžkach charakterizuje Planckova krivka.

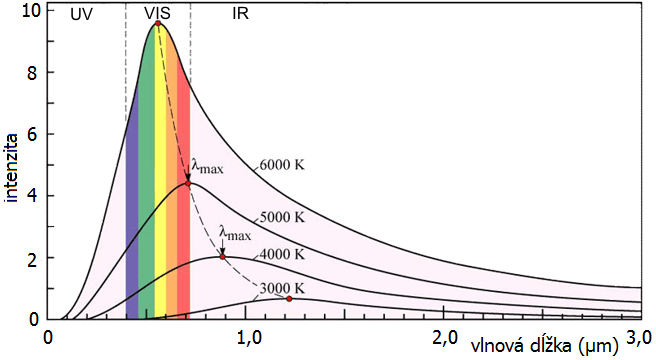Planckova krivka popisuje spektrálne rozdelenie intenzity žiarenia čierneho telesa pri vyznačených teplotách[4]. Z grafu je vidno, že s rastúcou teplotou sa vlnová dĺžka maximálneho vyžarovania skracuje a tiež sa zväčšuje množstvo vyžarovanej energie. To znamená, že ak sa povie, že nejaké žiarenie zodpovedá žiareniu čierneho telesa s teplotou x Kelvinov, tak spektrálna krivka tohto žiarenia bude Planckova krivka príslušnej vlnovej dĺžky.

Žiarenie väčšiny hviezd možno vo väčšine prípadov s dostatočnou presnosťou považovať za žiarenie čierneho telesa. Z toho vyplýva, že ak dve hviezdy majú rôzne teploty, vyžarujú na rôznych vlnových dĺžkach a teda majú aj rôzne farby.

Skutočne, ak sa pozrieme napríklad na hviezdu Rigel v súhvezdí Orión, ktorá má takmer 11 000 K, javí sa nám namodralá. Naopak, hviezda Betelguese v rovnakom súhvezdí má povrchovú teplotu necelých 4 000 K a javí sa ako silne načervenalá. Slnko s povrchovou teplotou okolo 6 000 K žiari na vlnovej dĺžke prislúchajúcej žltej farbe.