Algoritmizácia a programovanie - Slovne popísané algoritmy - O zločincoch a diamantoch :)

Traja zločinci ukradli diamanty. Po tomto náročnom dni boli všetci unavení, a preto sa rozhodli, že si diamanty rozdelia až ráno. V noci však jeden zločinec vstal a napadlo mu, že bude predsa lepšie, ak si svoj podiel vezme hneď. Rozdelil lup na 3 rovnaké hromady. Jeden diamant, ktorý zvýšil, dal strážcovi lupu, aby neprezradil ostatným dvom, čo urobil. Ukryl svoju kopu a opäť si ľahol spať. Neskôr vstal aj druhý zločinec a urobil to isté. Taktiež mu zvýšil jeden diamant a ten dal takisto strážcovi lupu, aby ho neprezradil. Napokon vstal aj tretí zločinec a postupoval rovnako ako prví dvaja (zvyšný diamant dal tiež strážcovi). Ráno, keď zločinci vstali, rozdelili si zostávajúcu kopu a diamant, ktorý zvýšil, dali strážcovi za „stráženie“. Aký najmenší počet diamantov mohli zločinci ukradnúť?

Pri riešení tejto úlohy sme použili zopár rovníc. Rovnice tohto typu sa nazývajú diofantovské, podľa gréckeho matematika Diofanta, ktorý ich ako prvý použil pri riešení niektorých, nielen matematických, úloh.

Pre lepšie predstavenie situácie sme si načrtli obrázok so zmenšujúcimi sa hromadami diamantov.

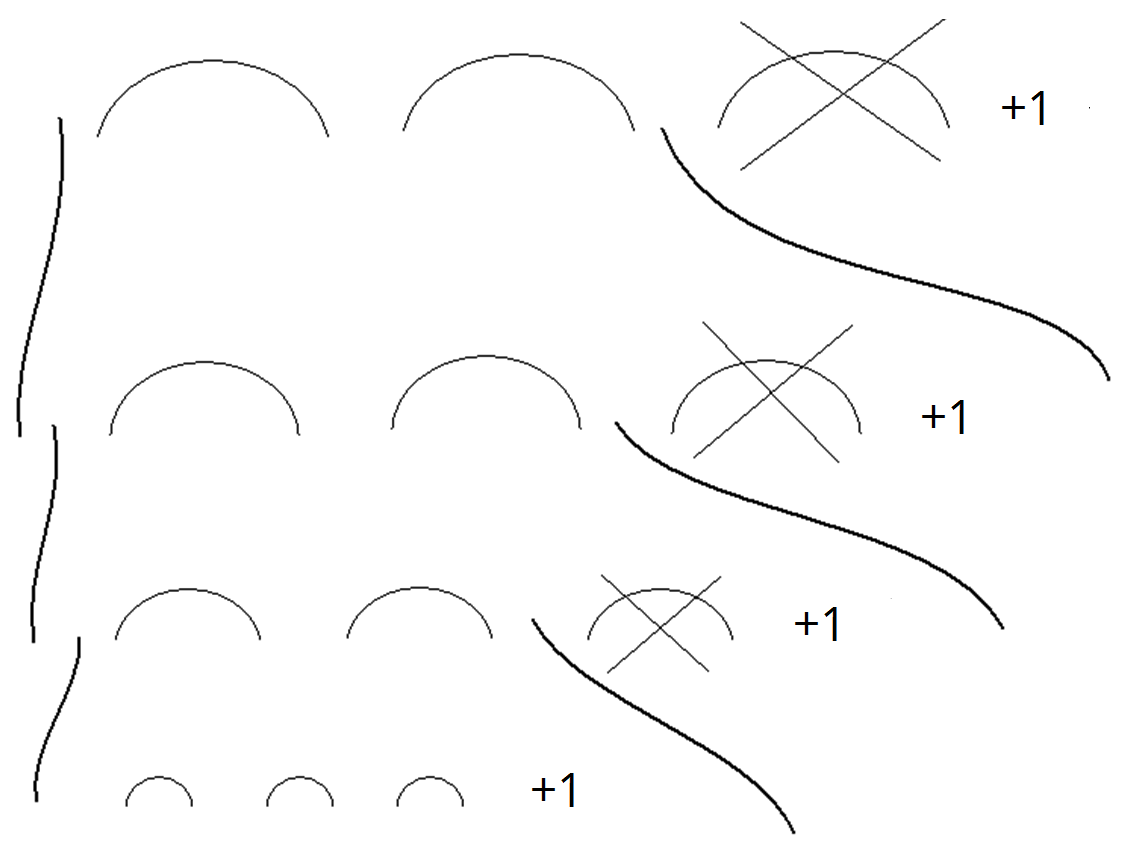Nakreslená základná myšlienka algoritmu

Vieme, že keď prvý zločinec vstal, rozdelil kopy na tri časti a svoj podiel si vzal, zostal jeden diamant navyše. Táto situácia je na našom obrázku znázornená v prvom (hornom) rade kôp diamantov. Podobne je znázornený aj druhý, aj tretí rad, ibaže s menším počtom diamantov (po odobratí jednej kopy prvým zločincom už druhý zločinec rozdeľuje iba zo zvyšného počtu diamantov, teda zo zvyšných dvoch kôp, na ktoré ich rozdelil prvý zločinec). To sme si tiež znázornili do obrázka. Takto sú zakreslené všetky delenia, pričom v poslednom rade si už kopu delia všetci zločinci.

Pomocou tohto obrázka si môžeme odvodiť prvú rovnicu. Ak a bude počet diamantov jednej kôpky v poslednom rade, teda počet, ktorý dostal jednotlivý zločinec po záverečnom delení, tak môžeme povedať, že počet diamantov pred týmto delením bol b. Čiže:

b = (3 * a) + 1

Vieme, že počet týchto diamantov b je vlastne dvomi kopami z delenia, ktoré spravil tretí zločinec. Takže b/2 je jedna kopa z tohto delenia. A z toho nám vyplýva ďalší vzorec, a to počet diamantov pred tretím delením (c). A to je:

c = (3 * b/2) + 1

Ďalej vieme, že tento počet diamantov c je znova dvomi kopami, ktoré už pred tým spravil druhý zločinec, a jedna kopa má teda počet diamantov c/2. Čiže môžeme zapísať ďalší vzorec pre počet diamantov pred druhým delením (d):

d = (3 * c/2) + 1

Napokon sa dostávame k prvému zločincovi, pri ktorom pomocou predošlých postupov zistíme, že po rozdelení kôp mala jedna kopa d/2 diamantov. Výsledkom posledného vzorca je vlastne počet všetkých diamantov, ktoré zločinci ulúpili (n). Takže platí, že:

n = (3 * d/2) + 1

Ak za d v poslednej rovnici dosadíme predchádzajúci vzorec, kde máme d vyjadrené, a do nej dosadíme zasa c, ktoré je vyjadrené ešte v predchádzajúcom vzorci, a do neho opäť dosadíme b z ešte predchádzajúceho vzorca, dostaneme:

n = (3 * ((3 * ((3 * ((3 * a) + 1) /2) + 1) /2) + 1) /2) + 1

Po matematických úpravách:

n = (3 * ((3 * ((9 * a)/2 + 5/2) /2) + 1) /2) + 1

n = (3 * (((27 * a)/4 + 15/4) + 1) /2) + 1

n = (3 * ((27 * a)/4 + 19/4) /2) + 1

n = (((81 * a)/4 + 57/4) /2) + 1

n = ((81 * a)/8 + 57/8) + 1

n = (81 * a)/8 + 65/8

získame výsledný vzťah:

n = ((81 * a) + 65) /8

Po tomto odvodení je na nás, aby sme dosádzali za neznámu a (počet diamantov v kope z posledného radu) celé čísla od 1 až pokým n nebude celé číslo (nie desatinné, pretože diamanty nikto „nelámal“). Po chvíli sme zistili, že najmenší počet diamantov, ktorý mohli zločinci ukradnúť, bol 79.

Program O zločincoch a diamatoch

Hodnotenie užitočnosti článku:

• ← Algoritmizácia a programovanie - Slovne popísané algoritmy - Mince :)
• Algoritmizácia a programovanie - Slovne popísané algoritmy - Výmena obsahu dvoch pohárov :) →