Hydrostatický tlak, hydrostatický paradox :)

Tlak vyvolaný tiažovou silou v kvapaline.

Máme nádobu naplnenú kvapalinou hustoty ρ. V hĺbke h si myslíme plochu s obsahom S. Stĺpec kvapaliny pôsobí na plochu tiažovou silou:

• F_g – tiažová sila [N],
• S – plocha [m²],
• h – hĺbka alebo výška stĺpca kvapaliny [m], 
• ρ – hustota kvapaliny [kg/m³], 

a vyvolá hydrostatický tlak:

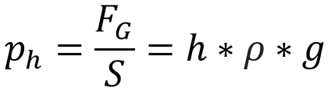• p_h – hydrostatický tlak [Pa], 
• F_g – tiažová sila [N],
• S – plocha [m²],
• h – hĺbka alebo výška stĺpca kvapaliny [m], 
• g – gravitačné zrýchlenie [m/s²],
• ρ – hustota kvapaliny [kg/m³]. 

Pre naše zemepisné šírky je hodnota g 9,81 [m/s²].

Hydrostatický tlak inak:

• je tlak v kvapaline, ktorý je vyvolaný vlastnou tiažou kvapaliny,
• závisí iba od hustoty kvapaliny a hĺbky pod povrchom kvapaliny,
• nezávisí ani od tvaru ani veľkosti nádoby,
• hydrostatický tlak sa vyskytuje aj v plynoch, vtedy však hovoríme o aerostatickom tlaku,
• matematickým vyjadrením hydrostatického tlaku je vzorec: p_h = h × g × ρ, kde h je hĺbka kvapaliny, v ktorej meriame tlak, g je gravitačná konštanta, ρ je hustota kvapaliny,
• jednotkou hydrostatického tlaku je Pa,
• čím je kvapalina hustejšia, tým je hydrostatický tlak väčší,
• čím je hĺbka kvapaliny väčšia, tým je hydrostatický tlak väčší.

x

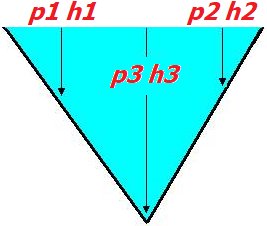
Hydrostatický paradox:

• je vyjadrením jednej z vlastností hydrostatického tlaku, konkrétne tej, že nezávisí od objemu, resp. od hmotnosti (vo všeobecnosti od množstva) kvapaliny,
• v praxi to znamená toľko, že ak máme tri nádoby, ktoré majú rôzny objem, ale sú naplnené kvapalinou do rovnakej výšky, tak hydrostatický tlak bude v každej tejto nádobe rovnaký.

Hydrostatický paradox

Prístroj na meranie hydrostatického tlaku	Ukážka merania

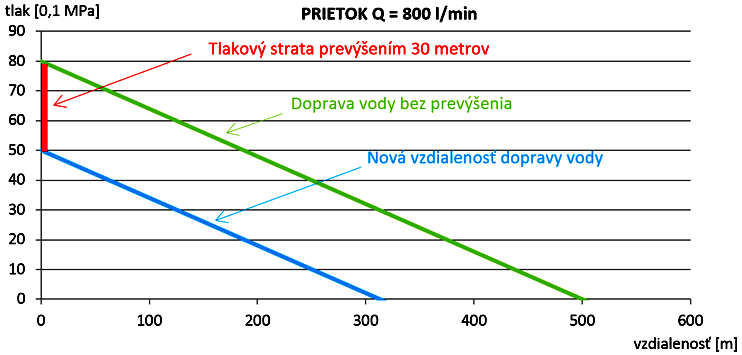Znázornenie vplyvu tlakovej straty prevýšením na vzdialenosť dopravy vody

Hydrostatický paradox podľa Wikipédie:

Hydrostatický paradox  je označenie skutočnosti, že sila pôsobiaca na dno nádoby od hydrostatického tlaku nie je závislá od tvaru nádoby a môže byť odlišná od tiaže objemu kvapaliny v tejto nádobe. 

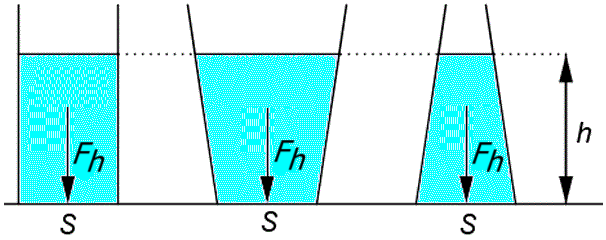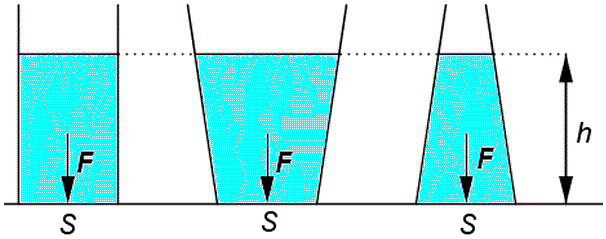
Ak do rôzne tvarovaných nádob (pozri horný obrázok) s rovnakým obsahom dna nalejeme rovnakú kvapalinu do rovnakej výšky, objem kvapaliny a teda aj jej tiaž bude najmenšia v zužujúcej sa nádobe a najväčšia v rozširujúcej. Napriek tomu bude na dno pôsobiť vo všetkých nádobách rovnaká sila od hydrostatického tlaku: 

F_h = ρ * g * h * S 

• F_h – sila od hydrostatického tlaku (N)
• ρ – hustota kvapaliny (kg * m⁻³)
• h – výška hladiny (m)
• S – plocha dna nádoby (m²) 

Tento zdanlivý nesúlad (paradox) je spôsobený reakčnými silami v šikmých stenách nádob.

Hodnotenie užitočnosti článku:

• ← Hydrospracovateľský (logický) člen ALEBO (OR) :)
• Ideálna kvapalina :) →