Karnaughove mapy, susediace členy :)

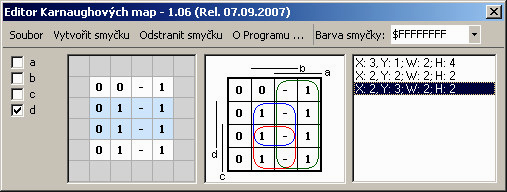
Metóda minimalizácie logickej funkcie pomocou špeciálnych tabuliek, tzv. Karnaughových máp. 

x

Ide o uniformnú techniku, pomocou ktorej dostaneme minimálny výraz logickej funkcie.

Systém Karnaughovej mapy je založený na pravidle Booleovej algebry, že dva členy logického výrazu, ktoré obsahujú tie isté premenné a líšia sa iba v jednej premennej sú redukovateľné.

T.j. možno ich zjednodušiť tak, že vynecháme premennú v ktorej sa líšia, čiže:

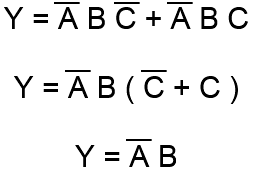Dva členy, ktoré sa líšia iba v jednej premennej sa nazývajú susediacimi členmi a v Karnaughovej mape sa nachádzajú vedľa seba.

Karnaughová mapa je zvláštnou formou pravdivostnej tabuľky logickej funkcie. Je to tabuľka vytvorená v poli štvorcov, kde každý štvorec reprezentuje jednu danú kombináciu vstupov. Karnaughová mapa sa napĺňa zapisovaním hodnôt funkcie pre každú z kombinácií.

Napríklad pre logickú funkciu

je pravdivostná tabuľka v ktorej sú na ľavej strane zapísané všetky kombinácie troch vstupných logických premenných A, B a C a na pravej strane pre výstupnú premennú Y zapísané jednotky iba pre tie kombinácie, ktoré sa nachádzajú na pravej strane logickej funkcie:

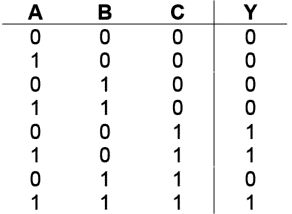a Karnaughová mapa tejto funkcie:

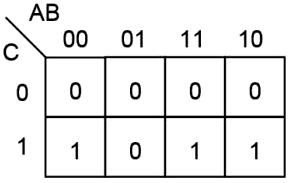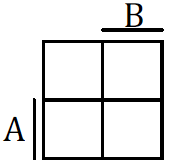
Každé dva susedné štvorce v Karnaughovej mape reprezentujú susedné kombinácie (kombinácie susedných členov), ktoré sa líšia iba v jednej premennej (00 01 11 10). Podobne kombinácia prvého riadku je susednou kombináciou posledného riadku. Tabuľka môže byť chápaná ako povrch guľe. Rohy tabuľky sú si susedné. Podobne ako rohy na hracej kocke. 

Označenie premenných svorkami
Karnaughova mapa pre 1 premennú	x	Karnaughova mapa pre 2 premenné	x	Karnaughova mapa pre 3 premenné		Karnaughova mapa pre 4 premenné

Algebraické označenie premenných
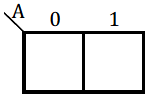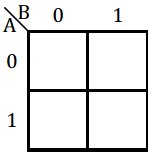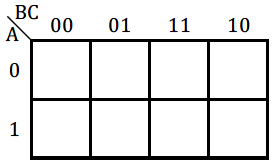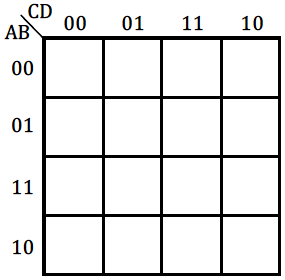Karnaughova mapa pre 1 premennú	x	Karnaughova mapa pre 2 premenné	x	Karnaughova mapa pre 3 premenné	x	Karnaughova mapa pre 4 premenné

Zdroje
Prevzaté a upravené z: 
• http://www.zarsoft.sk/2018/10/12/karnaughova-mapa/.

Hodnotenie užitočnosti článku:

• ← Jednosmerný elektrický prúd :)
• Katóda :) →