Booleova algebra podrobne :)

Vytvorené: 12. 11. 2013 Tlačiť

Algebra, v ktorej sú aritmetické operácie[1] nahradené logickými operáciami, ako AND, OR a NOT a s číslami sa pracuje v binárnom vyjadrení.

Autorom Booleovej algebry je filozof a matematik George Boole (1815-1864). Algebru a logiku spojil vo svojej knihe Skúmanie zákonov myslenia z roku 1854. V tom čase nepovšimnutá, hrá jeho algebra dodnes významnú úlohu v oblasti počítačov.

Booleova algebra inak:

Booleova algebra slúži na matematický opis zákonov a pravidiel výrokovej logiky, ktorá rieši vzťahy medzi pravdivými a nepravdivými výrokmi.

Pravdivému výroku prideľujeme logickú hodnotu 1, nepravidelnému výroku logickú hodnotu 0. Nositeľom elementárnej informácie o pravdivosti alebo nepravdivosti výroku je logická premenná, ktorá môže nadobúdať dve hodnoty: 0 a 1.

Booleova algebra ešte inak:

Časť matematiky, ktorá sa používa na analýzu logických sústav.

Výpočty v BA sa opierajú o predpoklad, že logické sústavy môžu nadobúdať iba dva stavy:

pravdivý,
nepravdivý.

Pravdivosť a nepravdivosť sú dané dvoma logickými hodnotami, ktorým sa v číslicovej technike priraďujú číslové hodnoty 0 a 1.

Booleova algebra umožňuje opis vzťahov medzi stavmi v číslicovom obvode v tvare výrazov (logických funkcií) zapísaných podobne ako v obyčajnej algebre.

Booleova algebra podrobne:

Booleova algebra je vetvou matematiky pomenovanou podľa anglického logika a matematika Georga Boolea, ktorý ako prvý publikoval práce z tejto oblasti.

Booleova algebra nie je algebra čísel, s ktorou sa stretávame v matematike. Je to algebra logických stavov. Vzhľadom ku klasickej algebre je preto inak definovaná, napríklad v nej vôbec nenájdeme operácie odčítania a delenia[2].

Základné funkcie Booleovej algebry sú:

logický súčet OR,
logický súčin AND,
negácia NOT.

Medzi základné pravidlá Booleovej algebry patria:

A plus 0 je vždy A, ak je A=1 je to 1, ak je A=0 je to 0.

A krát 0 je vždy 0.

A plus 1 je vždy 1 bez ohľadu, akú logickú hodnotu má A.

A krát 1 je vždy A, ak je A=1 je to 1, ak A=0 je to 0…

V Booleovej algebre pre logický súčet a logický súčin platia tieto zákony:

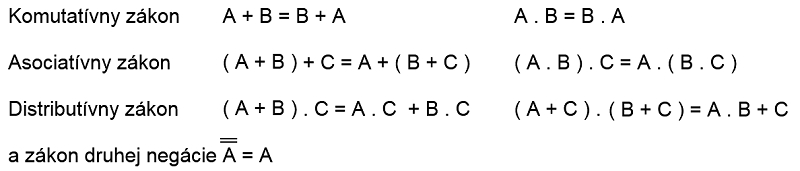Vlastnosťou Booleovej algebry je aj dualita. Ľubovoľnú logickú funkciu možno vyjadriť vhodným postupom aj v inom – duálnom tvare. O tejto vlastnosti pojednáva De Morganov zákon, ktorý hovorí že logickú funkciu NAND je možné vyjadriť v inom – duálnom tvare pomocou negácie a funkcie OR a opačne, logickú funkciu NOR je možné vyjadriť v inom – duálnom tvare pomocou negácie a logickej funkcie AND.

Dualita logických hradiel AND a OR

Shannov teorém zobecňuje De Morganov zákon a hovorí, že každá logická funkcia, ktorá obsahuje logické premenná A, B, C…, medzi ktorými sú operácie logického sčítania OR a logického násobenia AND sa dá napísať v inom – duálnom tvare ako funkcia, ktorá obsahuje pôvodné logické premenné A, B, C…, ale negované a logické operácie OR a AND sa medzi sebou vymenia.

Kanonický tvar tohoto teorému môžeme napísať ako:

Napríklad pre logický výraz (A + C) × (B + C) = Y môžeme podľa Shannovho teorému napísať:

s použitím základných pravidiel Booleovej algebry môžeme ďalej písať:

ak na túto logický rovnicu aplikujeme Shannov teorém a s prihliadnutím na zákon druhej negácie, dostaneme:

Základné pravidlá a vlastnosť duality Booleovej algebry sa používajú a majú veľký význam pri navrhovaní a minimalizácií zložitejších logických funkcií a pri ich realizácií pomocou základných logických hradiel a integrovaných logických obvodov.

Ak realizovaná logická funkcia obsahuje prevažne logické operácie NAND, NOT a len jednu logickú operáciu OR a ak ostanú v niekoľkých puzdrách integrovaných obvodov voľné hradlá NAND a NOT, je zbytočné pridať kvôli jednej funkcii OR ďalšie puzdro integrovaného obvodu. Funkcia NOR sa dá zrealizovať (s prihliadnutím na duálnu vlastnosť Booleovej algebry) pomocou voľných hradiel NAND a NOT.