Prúdenie tekutiny, ustálené prúdenie, prúdnica, prúdové pole (prúdnicový model tekutiny), prúdové vlákno, prúdová trubica, hmotnostný tok, objemový tok, rovnica spojitosti toku (rovnica kontinuity) :)

Pod pojmom prúdenie tekutiny rozumieme pohyb tekutiny prevažne v jednom smere.

Fyzikálnymi zákonitosťami, ktorými sa riadi prúdiaca tekutina a silami pôsobiacimi na tuhé telesá nachádzajúce sa v prúdiacom tekutom prostredí sa zaoberá dynamika tekutín[1].

Štúdium prúdiacich kvapalín a plynov je veľmi zložité. Pri zjednodušenom opise javov a zákonitostí v prúdiacich tekutinách zanedbávame ich viskozitu a používame model dokonalej kvapaliny a dokonalého plynu.

Najjednoduchším prípadom prúdenia tekutiny je ustálené prúdenie (stacionárne). Vyznačuje sa tým, že v každom bode prúdiacej tekutiny je veľkosť a smer rýchlosti v prúdenia stály a nezávisí od času (v = konštanta).

Prúdnica je myslená čiara, ktorej tvar je taký, aby dotyčnica zostrojená v jej ľubovoľnom bode mala smer rýchlosti častice pohybujúcej sa tekutiny. Každým bodom prúdiacej tekutiny prechádza najviac jedna prúdnica. Prúdnice sa nemôžu navzájom pretínať. Hustotou prúdnic modelujeme veľkosť rýchlosti prúdiacej tekutiny. Prúdnicový model tekutiny nazývame prúdové pole.

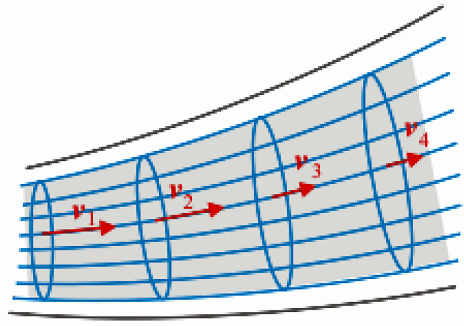Tekutina prúdiaca cez malú plochu v prúdovom poli sa nazýva prúdové vlákno. Všetky prúdnice zobrazujúce pohyb povrchových častíc prúdového vlákna tvoria prúdovú trubicu. Pretože sa prúdnice nikde nepretínajú, prúdiaca tekutina sa správa ako v potrubí s nepriepustnými stenami a nemôže cez jej povrch odtekať ani pritekať.

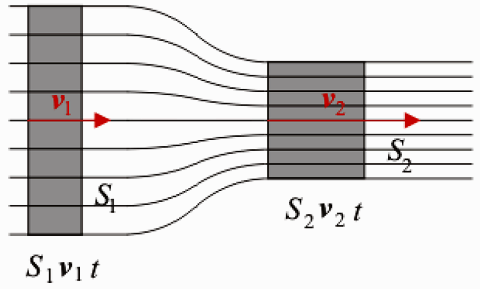Na obrázku je znázornené ustálené prúdenie ideálnej kvapaliny so stálou hustotou r v prúdovej trubici. Viskozita ideálnej kvapaliny je nulová, preto je veľkosť rýchlosti prúdenia v každom mieste prierezu prúdovej trubice rovnaká. Za čas Δt pretečie prierezom S₁ stálou rýchlosťou o veľkosti v₁ kvapalina s objemom

Objemový tok je veličina vyjadrujúca číselne objem kvapaliny, ktorý pretečie daným prierezom prúdovej trubice za časovú jednotku.

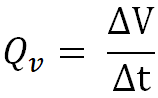Ideálna kvapalina je nestlačiteľná, preto pretečie prierezom S₂ prúdovej trubice za rovnaký čas Δt rýchlosťou s veľkosťou v₂ rovnaký objem

kvapaliny, ako kvapaliny, ako prierezom S₁. Objemový tok v uvažovaných prierezoch je rovnaký, preto platí vzťah

Z tohto vzťahu vyplýva, že ak sa prierez prúdovej trubice mení, mení sa aj rýchlosť prúdenia kvapaliny. Pre pomer rýchlostí prúdenia v dvoch rôznych prierezoch pritom platí

Objemový tok

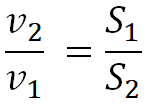v ideálnej kvapaliny je v celej prúdovej trubici rovnaký. Túto skutočnosť vyjadrujeme vzťahom:

Inak povedané: Zmenšenie obsahu prierezu potrubia má za následok zväčšenie rýchlosti prúdenia kvapaliny.

Hmotnostný tok je veličina vyjadrujúca číselne hmotnosť kvapaliny, ktorá prejde daným prierezom prúdovej trubice za časovú jednotku.

Rovnica spojitosti toku (rovnica kontinuity) vyjadruje, že pri ustálenom prúdení je hmotnostný tok tekutiny so stálou hustotou ρ v každom priereze prúdovej trubice rovnaký. Tento vzťah vyjadruje Zákon zachovania hmotnosti pre ustálené prúdenie tekutiny.

[1] Tvorí ju hydrodynamika a aerodynamika. 

x

Rovnica kontinuity

Hodnotenie užitočnosti článku:

• ← Protónové číslo prvku (Z, atómové číslo), nukleónové číslo prvku (A, hmotnostné číslo), izotopy, Bohrov model :)
• Prvky a zlúčeniny :) →