Minimalizácia logickej funkcie využitím Booleovej algebry a pomocou Karnaughovej mapy :)

Zložité logické funkcie je možné minimalizovať – zjednodušiť niekoľkými metódami. Napríklad:

• využitím Booleovej algebry,
• pomocou Karnaughovej mapy. 

Minimalizácia logickej funkcie použitím základných pravidiel Booleovej algebry.

Napríklad logickú funkciu:

s použitím pravidiel Booleovej algebry môžeme zapísať ako:

pričom podľa pravidiel Boolovej algebry platí pre:

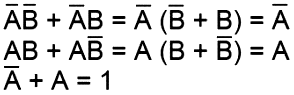môžeme napísať:

kde pre:

potom môžeme napísať:

Ako je z uvedeného príkladu vidieť, minimalizáciou logickej funkcie je možné výrazne zjednodušiť i na pohľad veľmi zložitý logický výraz. Minimalizácia logickej funkcie výrazne ušetrí logické hradlá pre jej realizáciu.

Pri získaní riešenia touto metódou nemusí ísť vždy o minimálne riešenie logickej funkcie. Každá logická funkcia si vyžaduje osobitný prístup a hľadania inej metódy pre jej vyriešenie. Výsledok zjednodušenia závisí taktiež od skúseností a schopností riešiteľa.

Minimalizácia logickej funkcie pomocou Karnaughovej mapy

Aby sme získali minimálnu funkciu pomocou Karnaughovej mapy musíme použiť a rešpektovať nasledovné pravidlá:

1. Skupiny susedných štvorcov, ktoré obsahujú jednotky sú označené v Karnaughovej mape nasledovným spôsobom:

• všetky jednotky zoskupíme do skupín,
• skupina musí obsahovať 2ⁿ štvorcov (1, 2, 4, 8, 16…),
• skupina musí mať tvar štvorca alebo obdĺžnika,
• vytvárame čo najväčšie skupiny,
• jeden štvorec môže byť zahrnutý do niekoľkých skupín,
• krajné stĺpce a krajné riadky sú si susedné.

2. Počet štvorcov v každej skupine je párne číslo okrem prípadu, keď skupina obsahuje jeden štvorec a premenné sa budú nachádzať vo všetkých štvorcoch s rovnakou hodnotou (buď 0 alebo 1) alebo s hodnotou 1 v jednej polovici a 0 v druhej polovici.

3. Každá skupina vytvorí zjednodušený člen, ktorého premenné nie sú predmetom zmeny pri kombinácií štvorcov v skupine.

4. Premenné sú v člene spojené operáciou logického súčinu AND.

5. Medzi členmi reprezentujúcimi skupiny je operácia logického súčtu OR.

Príklady Karnaughovej mapy pre logické funkcie: 

Príklad 1:

Karnaughová mapa s označením skupín:

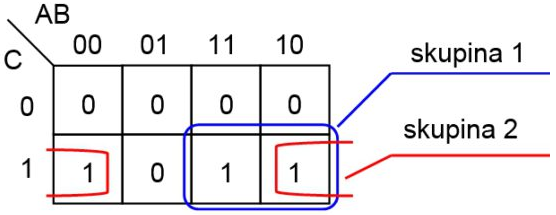Skupiny boli označené podľa horeuvedených pravidiel 1 a 2. Podľa pravidla, že každá skupina vytvorí zjednodušený člen, ktorého premenné nie sú predmetom zmeny pri kombinácií štvorcov v skupine a premenné sú v člene spojené operáciou logického súčinu môžeme pre prvú skupinu napísať zjednodušený člen

(premenná A je nad modrou oblasťou iba v stave 1, čiže ostáva ako A, premenná B je nad modrou oblasťou aj v stave 1 aj v stave 0, čiže vypadáva, premenná C je v modrej oblasti iba v stave 1, čiže ostáva ako C).

Podobne pre druhú skupinu napísať zjednodušený člen

(premenná A je nad červenou oblasťou aj v stave 1 aj v stave 0, čiže vypadáva, premenná B je nad červenou oblasťou iba v stave 0, čiže ostáva ako negovaná, premenná C je v červenej oblasti iba v stave 1, čiže ostáva ako C)

Podľa pravidla, že medzi členmi reprezentujúcimi skupiny je operácia logického súčtu je možné tieto dva členy spojiť logickou operáciou OR a pre minimalizovanú funkciu napísať:

Táto logická funkcia je minimalizovaná čo sa týka členov, ale nie je minimalizovaná čo sa týka realizácie pomocou hradiel. Môže byť ďalej zjednodušená pomocou distributívneho zákona do tvaru:

Pre jej realizáciu pomocou hradiel by sme potrebovali jeden negátor, jedno dvojvstupové hradlo OR a jedno dvojvstupové hradlo AND.

Príklad 2:

Karnaughová mapa logickej funkcie:

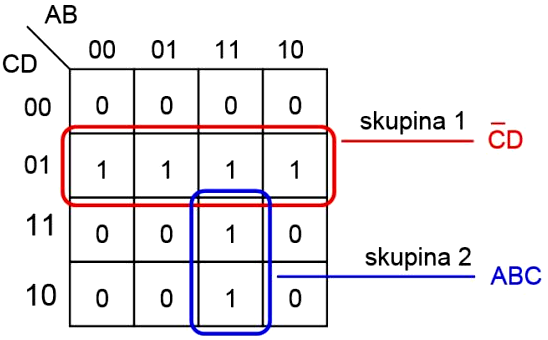Výsledok minimalizácie:

Príklad 3:

Karnaughová mapa logickej funkcie:

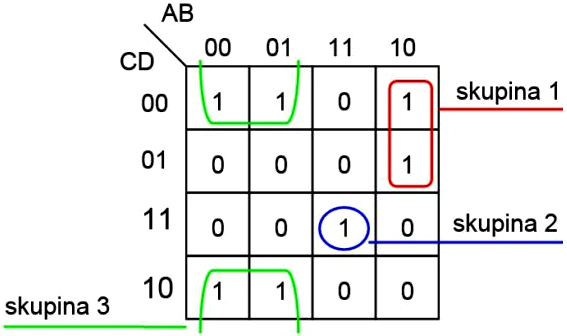Výsledok minimalizácie:

Príklad 4:

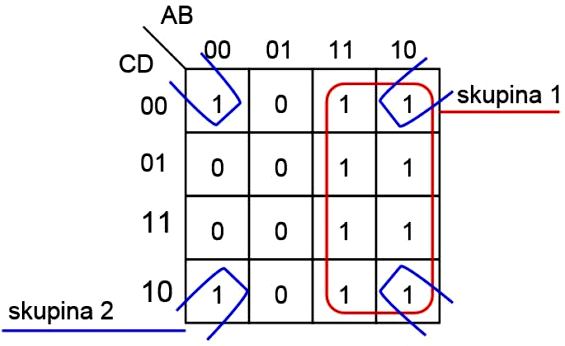Z príkladov je zrejmé, že čím väčšiu skupinu jednotiek v Karnaughovej mape je možné označiť do skupiny, tým viac členov logickej funkcie vypadne.

x

Aplikácia zákonov a pravidiel Booleovej algebry pri zjednodušení logickej funkcie

Zdroje
Prevzaté a upravené z: 
• http://www.zarsoft.sk/2018/10/12/karnaughova-mapa/.

Hodnotenie užitočnosti článku:

• ← Mikrohydraulika :)
• Mobilná hydraulika :) →